Problem n-królowych
Algorytmy z powrotami, OpenMP, wielowątkowość...

Problem n-królowych - Szacowanie wydajności algorytmu z powrotami
Analiza wyników
Wyniki otrzymane za pomocą metody Monte Carlo nie są już tak jednoznaczne jak
w przypadku omawianego wcześniej algorytmu z powrotami. Każda kolejna symulacja dla tej samej szachownicy może przynieść zupełnie inne rozwiązanie (szczególnie przy analizowaniu szachownic o dużych rozmiarach). Jednak najważniejszy jest fakt, że otrzymane rezultaty są bliskie prawdziwej liczbie sprawdzonych węzłów przez algorytm
z powrotami. I o ile trudno jest to stwierdzić w przypadku dużych szachownic, to przy mniejszych nie mamy z tym żadnego problemu (Tabela 1).
Tabela. 1. Porównanie ilości sprawdzonych węzłów przez algorytm z powrotami z ilością węzłów sprawdzonych, oszacowanych metodą Monte Carlo.
|
(n*n) |
przez algorytm z powrotami |
przez algorytm z powrotami (oszacowanie metodą Monte Carlo) |
|
|
61 | 59 |
|
|
221 | 227 |
|
|
895 | 860 |
|
|
3 585 | 3 786 |
|
|
15 721 | 15 580 |
|
|
72 379 | 78 830 |
|
|
348 151 | 364 300 |
|
|
1 806 707 | 1 750 000 |
|
|
10 103 869 | 10 230 000 |
|
|
59 815 315 | 52 945 154 |
|
|
377 901 399 | 326 900 154 |
|
|
2 978 040 571 | 2 776 209 012 |
|
|
? | 17 662 856 747 |
|
|
? | 145 624 254 307 |
Widzimy zatem, że oszacowanie ilości sprawdzonych węzłów dla małych szachownic jest bardzo dokładne. To pozwala nam sądzić, że i dla większych otrzymamy równie dobrze rezultaty. Przykładowo, dla szachownicy 16x16 nie znamy dokładnej liczby sprawdzonych węzłów, lecz szacujemy, że algorytm z powrotami będzie musiał przeanalizować ok. 6 razy więcej węzłów niż w przypadku szachownicy 15x15. Reasumując, dzięki metodzie Monte Carlo jesteśmy w stanie "przewidzieć" zachowanie testowanego algorytmu w czasie przetwarzania dowolnie dużej szachownicy.
Tabela. 2. Wyniki oszacowania ilości sprawdzonych węzłów dla szachownic o dużych rozmiarach
|
|
przez algorytm z powrotami (oszacowanie metodą Monte Carlo) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wraz ze wzrostem rozmiaru szachownicy, zwiększa się stopniowo ilość odwiedzonych węzłów.
Np. w czasie analizowania szachownicy 30x30, algorytm
z powrotami musiałby odwiedzić ok. 1,5 * 1011 razy więcej węzłów niż w przypadku szachownicy o rozmiarach 20x20.
Zaś przeanalizowanie szachownicy 100x100 jest równoznaczne ze sprawdzeniem o ok. 5 * 1015 razy więcej węzłów w
porównaniu do szachownicy 90x90. Ten stopniowy przyrost ilości sprawdzonych węzłów ilustruje wykres na rysunku 8.
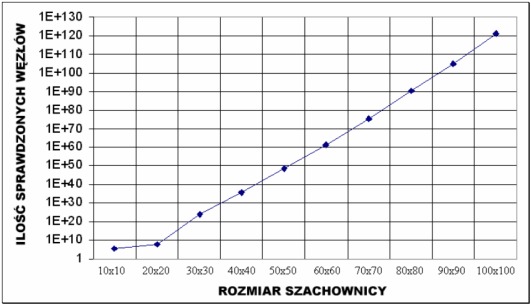
Rys 8. Szacunkowy przyrost ilości sprawdzonych węzłów w przypadku szachownic o dużych rozmiarach
Aby usprawnić analizę danych, napisałem aplikację, która generuje metodą Monte Carlo zbiór 20 oszacowań,
a następnie wylicza z nich średnią arytmetyczną. Efektem działania programu jest szacunkowa liczba węzłów
sprawdzonych przez algorytm z powrotami dla szachownicy o danym rozmiarze.
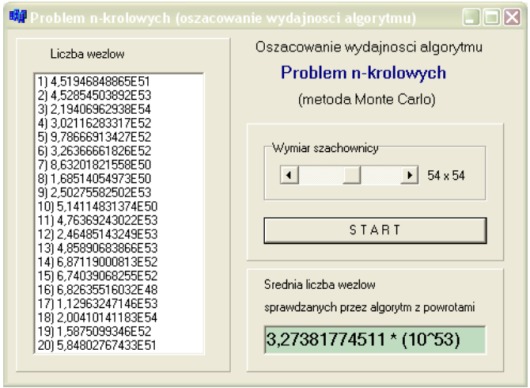
Rys 9. Przykładowe oszacowanie dla szachownicy 54x54
Biorąc pod uwagę wyniki badań, należy uznać, że algorytm Monte Carlo jest bardzo skuteczną metodą określania
wydajności algorytmu z powrotami. Oszacowanie złożoności obliczeniowej (a więc oszacowanie ilości sprawdzonych
węzłów), daje pewne wyobrażenie o liczbie węzłów, jakie (prawdopodobnie) musiałyby zostać sprawdzone przez algorytm
z powrotami. Oczywiście jest to "tylko" oszacowanie, jednak jak się okazuje, dosyć dokładne. Na jego podstawie
możemy przykładowo stwierdzić czy efektywność danego algorytmu nie spada gwałtownie przy przetwarzaniu bardzo
dużych struktur danych.
Jak się okazało, algorytm z powrotami dla problemu n-królowych zachowywałby się bardzo stabilnie przy analizowaniu
nawet bardzo dużych szachownic, a ilość sprawdzonych węzłów nie wrastałaby zbyt gwałtownie (Rys.8)