Problem n-królowych
Algorytmy z powrotami, OpenMP, wielowątkowość...

Problem n-królowych
Analiza wyników
Rozwiązanie problemu n-królowych, nie jest zadaniem łatwym. Największym problemem jest tutaj ogromna ilość węzłów
składających się na drzewo przestrzeni stanów. Algorytm, nie starający się przewidzieć, które węzły mogą doprowadzić
go do rozwiązania, nie ma szans na rozwiązanie problemu w sensownym czasie. Oczywiście zastosowanie algorytmu z
powrotami również nie jest wyjściem idealnym, jednak biorąc pod uwagę złożoność struktury danych, z jaką algorytm musi
się zmierzyć, można bez wahania powiedzieć, że jest to rozwiązanie bardzo efektywne. Na poparcie tej tezy przedstawię
porównanie złożoności obliczeniowej algorytmu naiwnego z algorytmem opartym na technice powrotów.
Algorytm naiwny testuje każdą kombinacje ustawień n-królowych na szachownicy n*n w nadziei, że któraś z nich przyniesie
oczekiwane rozwiązanie. Nie posiada mechanizmu analizowania węzłów w drzewie przestrzeni stanów, ponieważ tak naprawdę
drzewo w tym przypadku nie jest wcale generowane. Algorytm jest zatem zmuszony do przetestowania nn ustawień królowych,
co jest równoznaczne z przeanalizowaniem wszystkich węzłów w drzewie przestrzeni stanów. Z tego powodu złożoność
obliczeniowa algorytmu naiwnego jest bardzo wysoka, a wydajność bardzo niska. Zupełnie inną sytuację mamy w przypadku
algorytmu z powrotami. Otóż dzięki zastosowaniu strategii przeszukiwania w głąb połączonej z mechanizmem analizowania
węzłów i techniką powrotów, algorytm ten stanowi doskonałą alternatywę dla mało efektywnego algorytmu naiwnego.
Złożoność obliczeniowa algorytmu z powrotami jest bardzo niska, a ilość sprawdzonych węzłów to najczęściej ułamek
procenta wszystkich węzłów w drzewie przestrzeni stanów. Poza tym, odsetek węzłów sprawdzonych zmniejsza się wraz ze
wzrostem rozmiaru szachownicy (Tabela 1), więc ilość sprawdzonych węzłów rośnie wolniej niż ilość wszystkich węzłów w
drzewie przestrzeni stanów.
Tabela. 1. Ilość sprawdzonych węzłów w drzewie przestrzeni stanów przez algorytm z powrotami.
|
(n*n) |
w drzewie przestrzeni stanów |
węzłów |
sprawdzonych w całym drzewie |
|
|
341 | 61 | 17,8885630499% |
|
|
3906 | 221 | 5,6579621096% |
|
|
55987 | 895 | 1,5985853859% |
|
|
960800 | 3 585 | 0,3731265612% |
|
|
19173961 | 15 721 | 0,0819914049% |
|
|
435848050 | 72 379 | 0,0166064756% |
|
|
11111111111 | 348 151 | 0,0031333590% |
|
|
313842837672 | 1 806 707 | 0,0005756725% |
|
|
9726655034461 | 10 103 869 | 0,0001038781% |
|
|
328114698808274 | 59 815 315 | 0,0000182300% |
|
|
11966776581370200 | 377 901 399 | 0,0000031579% |
|
|
469172025408064000 | 2 532 748 321 | poniżej 0,0000000000% |
Aby wyznaczyć całkowitą liczbę węzłów w drzewie przestrzeni stanów należy zsumować ilość węzłów na każdym poziomie tego drzewa. Dla przykładu, jeśli poziomy zaczniemy liczyć od zera, to pierwszym napotkanym elementem będzie korzeń (więc na poziomie 0 mamy 1 węzeł). Na poziomie 1 jest n węzłów, zaś na poziomie 2 jest ich n2. Analogicznie na poziomie n jest nn węzłów. Można to ująć następującym wzorem:
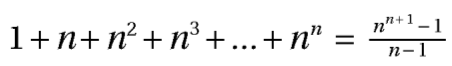
Po zestawieniu wyników w tabeli 1, widzimy jak bardzo wydajnym rozwiązaniem jest zastosowanie algorytmu z powrotami dla problemu
n-królowych. Aby przeanalizować klasyczną szachownicę o rozmiarze 8x8, której drzewo przestrzeni stanów składa się
z 19173961 węzłów, algorytm naiwny musiałby wygenerować wszystkie 16777216 ustawień królowych na szachownicy. Byłoby
to jednoznaczne z przeanalizowaniem całego drzewa przestrzeni stanów. Z drugiej strony, algorytm z powrotami w celu
odnalezienia wszystkich poprawnych kombinacji królowych, sprawdza jedynie 15721 węzłów
(ok. 0,08% wszystkich węzłów w drzewie). Przewaga strategii algorytmów z powrotami, nad algorytmem naiwnym jest więc niezaprzeczalna.
W zbiorze węzłów sprawdzonych przez algorytm z powrotami możemy wyznaczyć dwie zasadnicze grupy. Są to węzły obiecujące
i nieobiecujące. Najważniejszą grupą jest tutaj oczywiście grupa węzłów obiecujących. Zawiera się z niej jedynie niewielka
część wszystkich odwiedzonych węzłów w drzewie przestrzeni stanów, lecz to właśnie te węzły wyznaczają kierunek przeszukiwania
drzewa przestrzeni stanów i one też doprowadzają
w końcu do rozwiązania.
Wraz ze wzrostem rozmiaru szachownicy, wzrasta również ilość sposobów ustawienia na niej królowych.
Pewnym odstępstwem od powyższej normy jest szachownica o wymiarach 6x6, dla której istnieją tylko 4 sposoby
ustawienia królowych. Interesujące, że dla mniejszej szachownicy 5x5, możemy ustawić królowe na 10 sposobów,
a dla szachownicy o wymiarach 7x7 aż na 40 sposobów. Poza tym specyficznym przypadkiem regułą jest, że dla szachownicy
o wymiarach (n+1)*(n+1) istnieje więcej kombinacji ustawień królowych niż dla szachownicy o rozmiarze n*n.
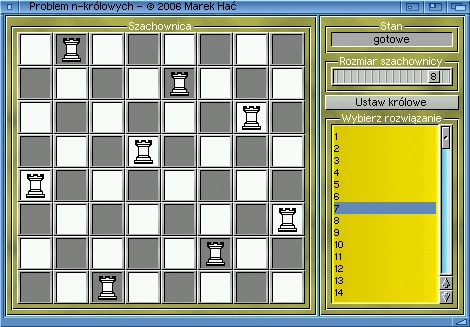
Rys 1. Przykładowe rozwiązanie problemu n-królowych dla szachownicy o wymiarach 8x8
(program uruchomiony
na komputerze Amiga)
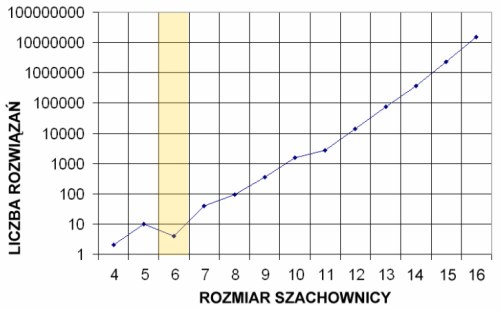
Rys 2. Liczba rozwiązań problemu n-królowych w zależności od rozmiaru szachownicy.
Kolejną ważną kwestią związaną z wydajnością rozważanego algorytmu jest jego złożoność czasowa. W przypadku
niewielkich szachownic (od 4x4 do 11x11) algorytm
z powrotami znajduje rozwiązanie niemal błyskawicznie (zależnie od prędkości procesora, jest to czas poniżej
jednej sekundy). Jednak już od szachownicy 12x12, ilość sekund konieczna do rozwiązania problemu gwałtownie
wzrasta. Dla przykładu, czas w jakim algorytm analizuje szachownicę o wymiarach 13x13, jest niemal siedmiokrotnie
dłuższy
w porównaniu do czasu poświęconego szachownicy 12x12. Za taki stan rzeczy odpowiada przede wszystkim ogromna
ilość węzłów w drzewie przestrzeni stanów. Mimo że algorytm z powrotami analizuje jedynie niewielką ich część,
to jednak przy tak obszernej strukturze danych, sprawdzenie nawet ułamka procentu wszystkich węzłów w drzewie
przestrzeni stanów może okazać się dla algorytmu bardzo czasochłonne. Poniżej znajduje się przykładowe rozwiązanie
problemu n-królowych dla szachownicy 15x15. Program został uruchomiony na komputerze wyposażonym w procesor Intel Celeron
taktowany zegarem o częstotliwości 2.00 GHz oraz 256 MB pamięci RAM. System operacyjny - Windows XP Home. Aby wyznaczyć
wszystkie 2279184 rozwiązania dla szachownicy 15x15 komputer pracował na "pełnych obrotach" przez niemal 20 minut.
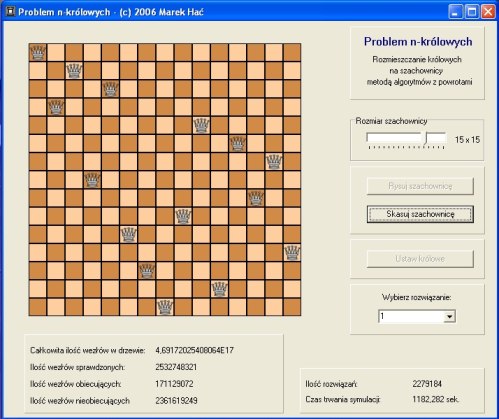
Rys 3. Przykładowe rozwiązanie problemu n-królowych dla szachownicy o wymiarach 15x15
(program uruchomiony pod kontrolą systemu Windows XP Home)
Program uruchomiony pod kontrolą systemu operacyjnego Windows/AmigaOS posłużył jedynie do wizualizacji problemu n-królowych.
Prawdzie testy mogły rozpocząc się dopiero po usunięciu graficznego interfejsu i uruchomieniu programu na jednej z
dystrybucji Linuxa. Aby jeszcze przyśpieszyć działanie testowanego programu,
uruchamiany był w środowisku tekstowym z pominięciem trybu graficznego.
Komputer, na którym dokonywałem symulacji składał się z procesora Intel Celeron D taktowanego zegarem o
częstotliwości 2.6 GHz, oraz 512 MB pamięci RAM. Na komputerze zainstalowany został system operacyjny
Fedora Core 6 z wersją jądra 2.6.18-1.2798.fc6. W skład systemu wchodził kompilator GCC w wersji 4.1.1.
Program uruchomiony na maszynie jednoprocesorowej (o podanej wyżej konfiguracji) jest w stanie analizować
wirtualne drzewo przestrzeni stanów z szybkością ok. 16 milionów wierzchołków na sekundę. Duża szybkość
testowania węzłów sprawia, że
w przeciągu dwóch setnych sekundy program potrafi wyznaczyć wszystkie możliwe ustawienia królowych na szachownicy
10x10. Dokładne pomiary czasu działania programu w trakcie przetwarzania szachownic o rozmiarach 4x4 - 16x16
przedstawione zostały
w tabeli 2.
Tabela. 2. Złożoność obliczeniowa programu rozwiązującego problem n-królowych na komputerze jednoprocesorowym.
|
|
|
|
|
|
|
|
0,000007 | 61 | 8 714 286 | 2 |
|
|
0,000016 | 221 | 13 812 500 | 10 |
|
|
0,000053 | 895 | 16 886 792 | 4 |
|
|
0,000197 | 3 585 | 18 197 970 | 40 |
|
|
0,000872 | 15 721 | 18 028 670 | 92 |
|
|
0,004158 | 72 379 | 17 407 167 | 352 |
|
|
0,020833 | 348 151 | 16 711 515 | 724 |
|
|
0,108324 | 1 806 707 | 16 678 732 | 2 680 |
|
|
0,616445 | 10 103 869 | 16 390 544 | 14 200 |
|
|
3,766299 | 59 815 315 | 15 881 722 | 73 712 |
|
|
24,632354 | 377 901 399 | 15 341 668 | 365 596 |
|
|
170,701428 | 2 532 748 321 | 14 837 300 | 2 279 184 |
|
|
1255,315929 | ? | 14 070 447 | 14 772 512 |